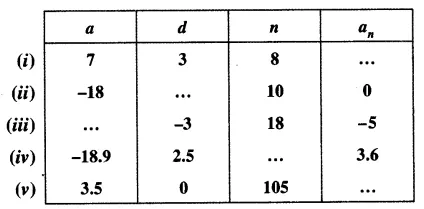
Solution:
(i) Given,
First term, a = 7
Common difference, d = 3
Number of terms, n = 8,
We have to find the nth term, an = ?
As we know, for an A.P.,
an = a + (n −1) d
Putting the values,
⇒ 7 + (8 − 1) 3
⇒ 7 + (7) 3
⇒ 7 + 21 = 28
Hence, an = 28
(ii) Given,
First term, a = -18
Common difference, d = ?
Number of terms, n = 10
nth term, an = 0
As we know, for an A.P.,
an = a + (n − 1) d
Putting the values,
0 = − 18 + (10 − 1) d
18 = 9 d
d = 18/9 = 2
Hence, common difference, d = 2
(iii) Given,
First term, a = ?
Common difference, d = -3
Number of terms, n = 18
Nth term, an = -5
As we know, for an A.P.,
an = a +(n − 1) d
Putting the values,
−5 = a + (18 − 1) (−3)
−5 = a + (17) (−3)
−5 = a − 51
a = 51 − 5 = 46
Hence, a = 46
(iv) Given,
First term, a = -18.9
Common difference, d = 2.5
Number of terms, n = ?
Nth term, an = 3.6
As we know, for an A.P.,
an = a +(n −1) d
Putting the values,
3.6 = − 18.9+(n − 1)2.5
3.6 + 18.9 = (n − 1)2.5
22.5 = (n − 1)2.5
(n – 1) = 22.5/2.5
n – 1 = 9
n = 10
Hence, n = 10
(v) Given,
First term, a = 3.5
Common difference, d = 0
Number of terms, n = 105
Nth term, an = ?
As we know, for an A.P.,
an = a + (n − 1) d
Putting the values,
an = 3.5 + (105 − 1) 0
an = 3.5 + 104 × 0
an = 3.5
Hence, an = 3.5