A spiral is made up of successive semicircles, with centres alternately at A and B

A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in Fig. 5.4. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take π = 22/)

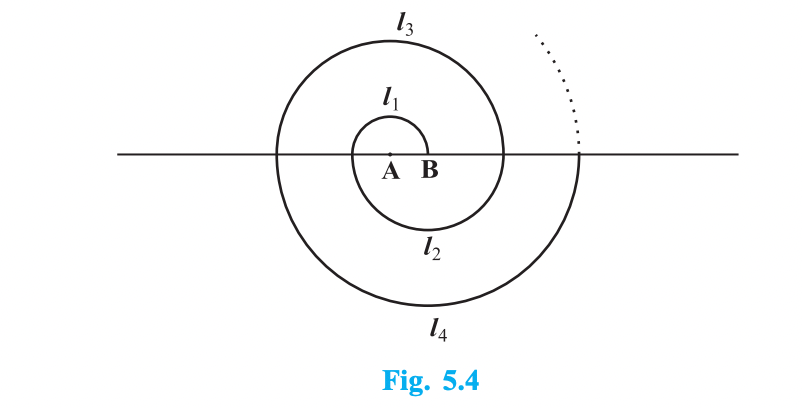
[Hint: Length of successive semicircles is l₁, l₂, l₃, l₄, . . . with centres at A, B, A, B, . . ., respectively.]

Solution:

We know,

The perimeter of a half-circle shape (as shown in the figure) = π r

Therefore,

l₁ = π(0.5) = π/2 cm

l₂ = π(1) = π cm

l₃ = π(1.5) = 3π/2 cm

Where, l_1, l₂, and l₃ are the lengths of the half-circle shapes.

Hence we have a series here, as,

π/2, π, 3π/2, 2π, ….

l₁ = π/2 cm

l₂ = π cm

Common difference, d = l₂ – l₁ = π – π/2 = π/2

First term = l₁= a = π/2 cm

By the sum of the n terms formula, we know,

S_n = n /2 [2 a + ( n – 1) d ]

Therefore, the sum of the length of 13 consecutive circles is;

S₁₃ = 13 /2 [2(π/2) + (13 – 1)π/2]

= 13 /2 [π + 6π]

=13 /2 (7π)

= 13 /2 × 7 × 22 /7

= 143 cm