Solution:
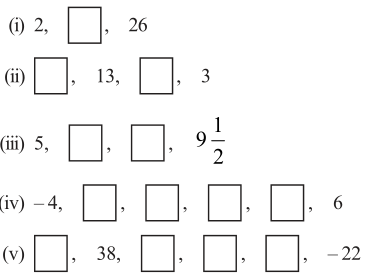
(i) For the given A.P., 2, _ 26
The first and third term are;
a = 2
a3 = 26
As we know, for an A.P.,
an = a + (n − 1) d
Therefore, putting the values here,
a3 = 2 + (3 – 1) d
26 = 2 + 2 d
24 = 2d
d = 12
a2 = a + d = 2 + 12 = 14
Therefore, 14 is the missing term.
(ii) For the given A.P. _, 13, _,3
a2 = 13 and
a4 = 3
As we know, for an A.P.,
an = a + (n − 1) d
Therefore, putting the values here,
a2 = a + (2 – 1) d
13 = a + d ………………. (i)
a4 = a + (4 – 1) d
3 = a + 3 d ………….. (ii)
On subtracting equation (i) from (ii), we get;
– 10 = 2 d
d = – 5
From equation (i), putting the value of d, we get;
13 = a + (-5)
a = 18
a3 = 18 + (3 – 1)(-5)
= 18 + 2(-5) = 18 – 10 = 8
Therefore, the missing terms are 18 and 8 respectively.
(iii) For the given A.P., 5, _, _ , 9 1/2
a = 5 and
a4 = 9 1/2 = 19/2
As we know, for an A.P.,
an = a + (n − 1) d
Therefore, putting the values here,
a4 = a + (4 – 1) d
19/2 = 5 + 3d
(19/2) – 5 = 3d
3d = 9/2
d = 3/2
a2 = a + (2 – 1) d
a2 = 5 + 3/2
a2 = 13/2
a3 = a + (3 – 1) d
a3 = 5 + 2 × 3/2
a3 = 8
Therefore, the missing terms are 13/2 and 8 respectively.
(iv) For the given A.P., -4, _, _, _, _, 6
a = −4 and
a6 = 6
As we know, for an A.P.,
an = a + (n − 1) d
Therefore, putting the values here,
a6 = a + (6 − 1)d
6 = −4 + 5 d
10 = 5d
d = 2
a2 = a + d = −4 + 2 = −2
a3 = a + 2d = −4 + 2(2) = 0
a4 = a + 3d = −4 + 3(2) = 2
a5 = a + 4d = −4 + 4(2) = 4
Therefore, the missing terms are −2, 0, 2, and 4 respectively.
(v) For the given A.P., _, 38, _, _, _, -22
a2 = 38
a6 = −22
As we know, for an A.P.,
an = a +( n −1) d
Therefore, putting the values here,
a2 = a + (2 − 1) d
38 = a + d ……………………. (i)
a6 = a + (6 − 1) d
−22 = a + 5 d …………………. (ii)
On subtracting equation (i) from (ii), we get
− 22 − 38 = 4d
−60 = 4d
d = −15
a = a2 − d = 38 − (−15) = 53
a3 = a + 2d = 53 + 2 (−15) = 23
a4 = a + 3d = 53 + 3 (−15) = 8
a5 = a + 4d = 53 + 4 (−15) = −7
Therefore, the missing terms are 53, 23, 8, and −7 respectively.