Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:

(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0

Solution:

(i) Given, x + y = 5 and 2x + 2y = 10

Comparing these equations with a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 we get,

(a₁/a₂) = 1/2

(b₁/b₂) = 1/2

(c₁/c₂) = 1/2

Here, (a₁/a₂) = (b₁/b₂) = (c₁/c₂)

∴The equations are coincident and they have an infinite number of possible solutions.

So, the equations are consistent.

For, x + y = 5 or y = 5 – x

x	0	3	5
y	5	2	0

For 2x + 2y = 10 or y = (10 – 2x)/2

x	0	3	5
y	5	2	0

So, the equations are represented in graphs as follows:

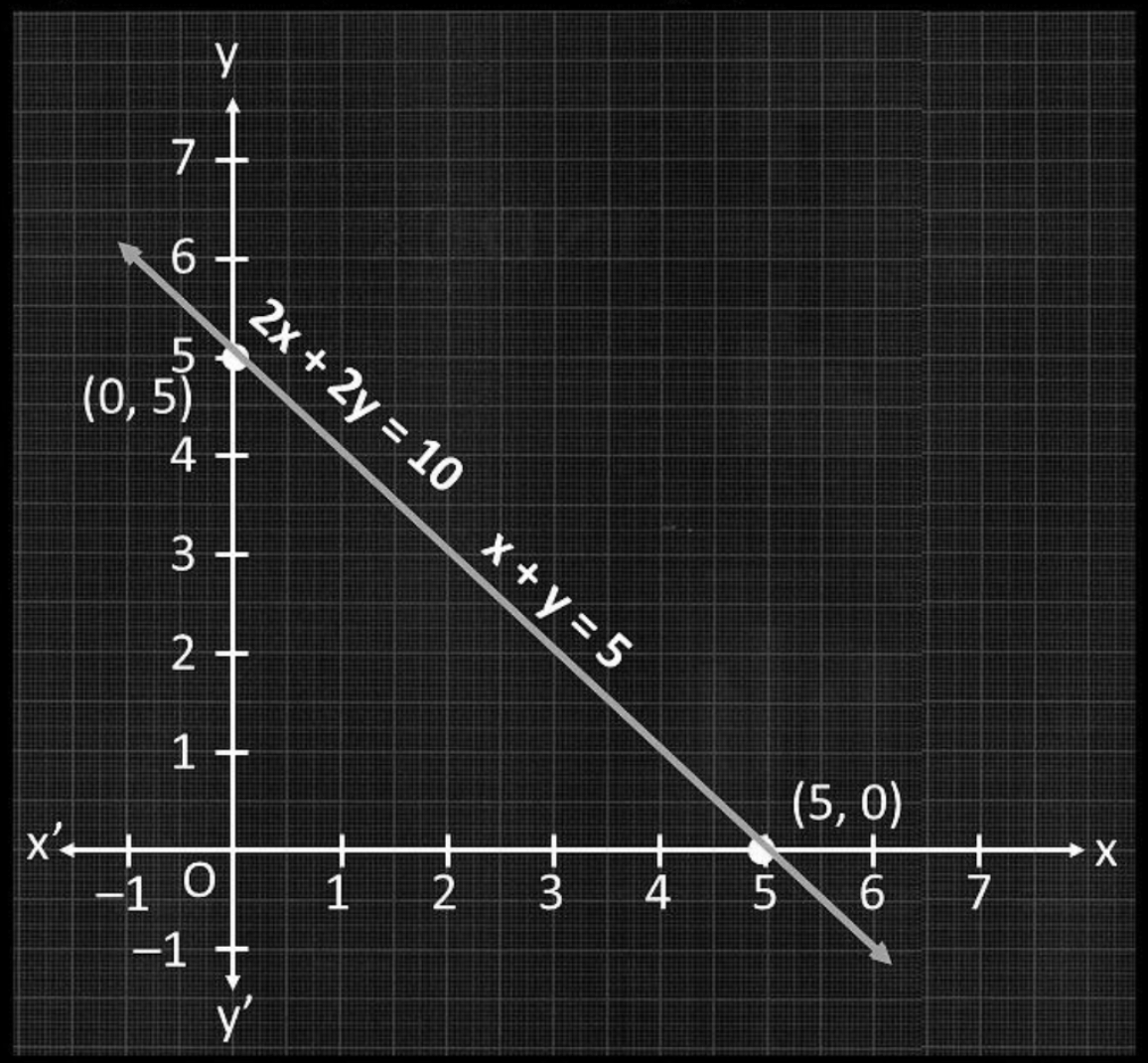
From the figure, we can see, that the lines are overlapping each other.

Therefore, the equations have infinite possible solutions.

(ii) Given, x – y = 8 and 3x – 3y = 16

Comparing these equations with a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 we get,

(a₁/a₂) = 1/3

(b₁/b₂) = -1/-3 = 1/3

(c₁/c₂) = 8/16 = 1/2

Here, (a₁/a₂) = (b₁/b₂) ≠ (c₁/c₂)

The equations are parallel to each other and have no solutions. Hence, the pair of linear equations is inconsistent.

(iii) Given, 2x + y – 6 = 0 and 4x – 2y – 4 = 0

Comparing these equations with a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 we get,

(a₁/a₂) = 2/4 = ½

(b₁/b₂) = 1/-2

(c₁/c₂) = -6/-4 = 3/2

Here, (a₁/a₂) ≠ (b₁/b₂)

The given linear equations are intersecting each other at one point and have only one solution. Hence, the pair of linear equations is consistent.

Now, for 2x + y – 6 = 0 or y = 6 – 2x

x	0	1	2
y	6	4	2

And for 4x – 2y – 4 = 0 or y = (4x – 4)/2

x	1	2	3
y	0	2	4

So, the equations are represented in graphs as follows:

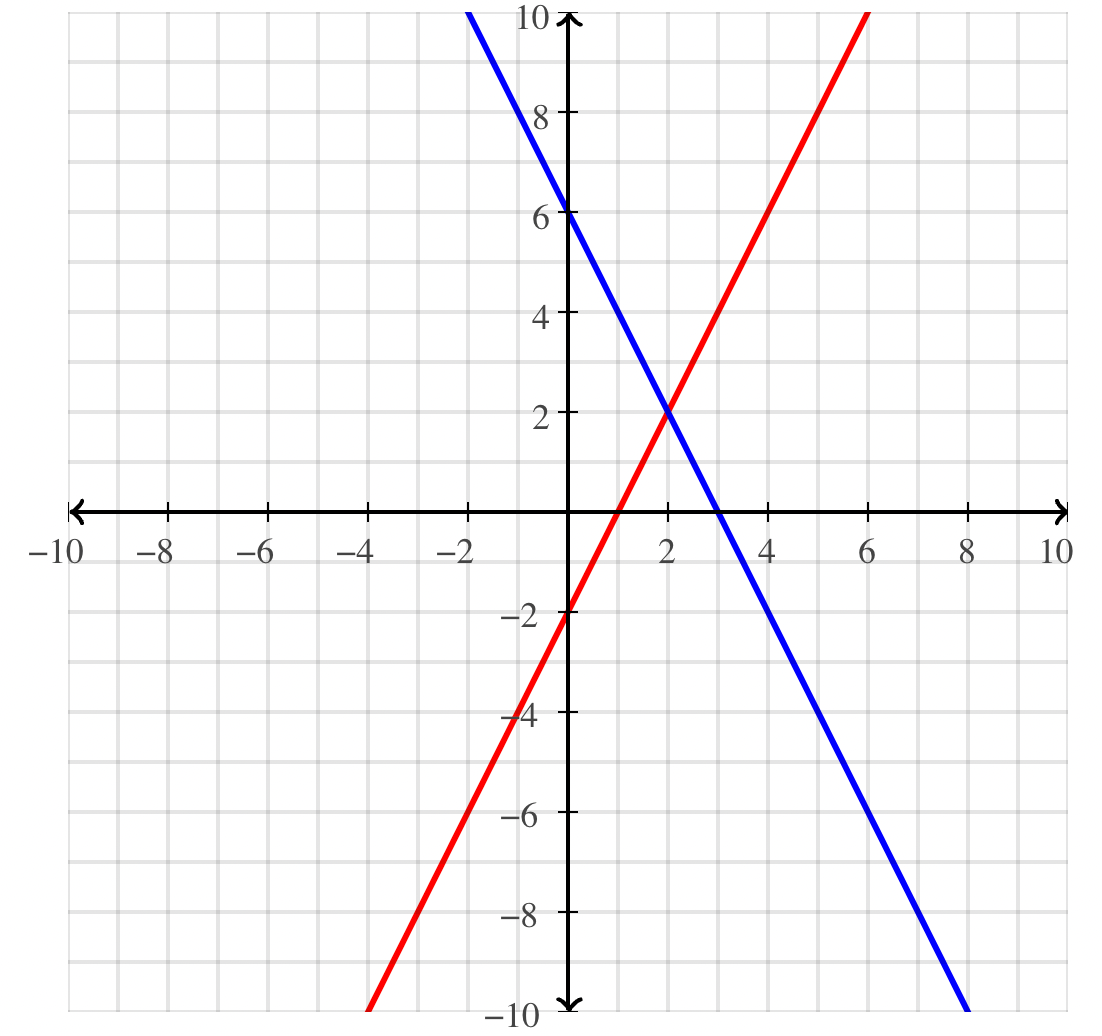
From the graph, it can be seen that these lines are intersecting each other at only one point,(2,2).

(iv) Given, 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0

Comparing these equations with a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 we get,

(a₁/a₂) = 2/4 = ½

(b₁/b₂) = -2/-4 = 1/2

(c₁/c₂) = 2/5

Here, (a₁/a₂) = (b₁/b₂) ≠ (c₁/c₂)

Thus, these linear equations have parallel and have no possible solutions. Hence, the pair of linear equations are inconsistent.